从one-hot encoding 到 word2vec 的理解
一、Word representation
在自然语言处理中,我们研究的基础是词语。但是计算机无法直接处理这些字符,因此,我们需要某种方法可以让我们对这些词语进行表示。
那在这里,我们就讨论两种情况:
1、 one-hot encodings
2、 dense embedding vectors
1.1 one-hot encodings

如上图所示, 当我们考虑在一个容量为 $40,000$ 的单词表中用向量表示单词,一个很直观地想法就是,构建一个 $40,000$ 维的向量,然后,不同的维度表示不同的单词。比如 第 $5391$ 维表示 Man, 第 $9853$ 维表示 Woman , 第 $4914$ 维表示 King, 等等。
这种表示方法固然简单,但它却有一个很致命的缺陷就是:
它把单词之间的关系给完全独立开来了。每个单词都是一个独立的个体,各个单词之间没有任何关联。这样的做法就让我们无法求出相似的单词。
比如:
I want a glass of orange ___
我们的算法通过学习语料库直到了横线处应该填写 juice, 但是,让我们看另外一个例子
I want a glass of apple ___
从直觉上来说,我们在这里应该也填 juice, 但是如果 apple juice 在语料库中出现的比较少,那么我们的模型很可能无法求出这个横线应该填 juice。
出现这种情况的原因是:one-hot encoding 会让任意两个单词的向量内积为0 所以,模型才无法学到其实 apple 和 orange 其实是蛮相近的。
1.2 dense embedding vectors
刚才说了, one-hot encoding 有着这么致命的缺点,那我们是不是可以想个办法,来克服这个缺陷,让相同意思的向量单词的 $cos$ 值尽可能的大。
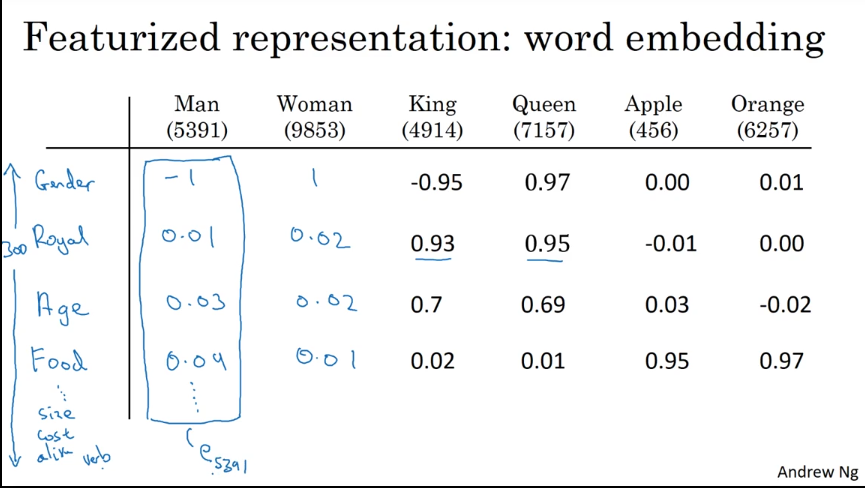
于是,我们就有了 dense embedding vectors ,我们先对语料库中的单词抽取一些特征,如下图所示:
我们抽取 Gender、Royal、Age、Food、Size、Cost、Verb … … 一共 300 个特征。然后再利用模型去学习各个单词对应特征上的值,最终使得每个单词都可以被一个维度为300的向量表示。比如 Man 可以表示成 $(-1, 0.01, 0.03, …, 0.09) \in \mathbb{R}^{300}$
这时候,我们再碰到上面的问题,模型可以自动的选择 juice 填入,因为 apple 和 orange 的向量表示是相近的,这样,会让模型觉得,上一个输入的单词是带有噪音的orange 所以,模型还是会选择填上juice。
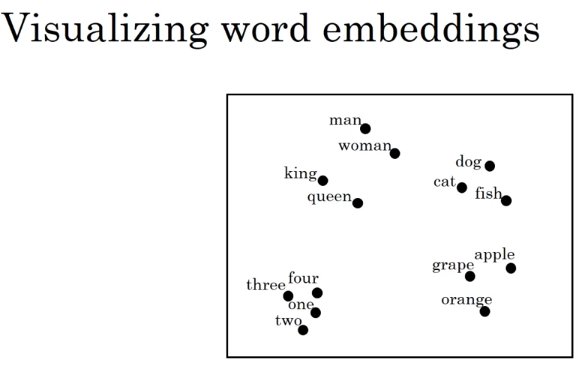
这时候我们通过 t-SNE 算法进行降维,画在平面上。可以很清晰的看出各个单词之间的相近程度。
二、Word Embedding
2.1 Embedding matrix

PS:来自NG的灵魂作画… …
我们想得到 dense vectors ,有一个比较常规的做法就是, 使用 Embedding Matrix ,假设我们现在的语料库有 $10, 000$ 个单词,每个单词可以用 one-hot encoding 的形式表示为 $O_j, j=1, 2, 3, …., 10000$, 然后,我们希望把这 one-encoding vecotr 可以转变成 维度为 300 的 dense vectors, 而且,运气非常好的是,我们通过某种学习方法学到了一个 Embedding Matrix $E$ 这个矩阵的形状是 $300 \times 10000$。
这时,我们想要得到一个 dense vectors 直接让 $E \cdot O_j = e_j$ 就可以获得该单词对应的 dense vector.
2.2 Learning word embeddings
OK,上面已经说过了,当我们获得 Embedding Matrix 的时候,我们就可以获得单词的 dense vector了,所以,现在就让我们想想办法怎么样去求这个 Embedding Matrix $E$
2.2.1 Neural Language Model
首先,我们先介绍一下,什么是 Language Model.
通常来说,Language Modeling 描述的是这样一类任务,在该任务中我们需要给某句话赋予概率(比如,在句子中看到 the lazy dog barked loudly ? 的概率是多少?);除了上述任务,我们还可以在给定上下文(后面用 context 表示)的情况下,去预测接下来的单词是给定单词的概率是多少(the lazy dog 后面出现 barked 的概率是多少?)
Note:
接下来的公式中,为了书写方便,我们使用 $P(w_{1:n})$ 代替 $P(w_{1}, w_{2}, w_{3}, …, w_{n})$
所以,Language Model 用公式来表示就是:
$$P(w_{1:n}) = p(w_{1}) P(w_{2} | w_{1}) P(w_{3} | w_{1:2}) P(w_{4} | w_{1:3}) … P(w_{n} | w_{1:n-1})$$
上述公式的意义就是,我们给定了 $n-1$ 个字符,那么,我们想要求出第 $n$ 个字符的概率。
对于现实生活中,我们通常采用马尔科夫假设,也就是第 $n$ 个词出现的概率只跟前 $k-1$ 个词有关,而不是跟前 $n-1$ 词都有关。
所以上述公式可以简化成
$$P(w_{1:n}) \approx \prod_{i=1}^n P(w_{i} | w_{i-k:i-1})$$
OK,语言模型简单的介绍完了,我们接下进入这一小节的重点, Bengio 大佬 2003 年的 Neural Language Model, 这个模型就可以用来训练我们在 2.1 节中所讲的那个 Embedding Matrix.
整个模型的结构如图所示:

模型的输入是前 $k$ 个单词,在上图的例子中 $k=6$ ,模型的输出是下一个单词的概率分布。
我们假设语料库中一共有 $10,000$ 个单词
这里的每一个单词的原始形式是 $o_j$ (one-hot encoding),经过一个 Embedding Matrix $E$ 之后,我们得到了它所对应的 dense vector $e_j \in \mathbb{R}^{300}$ (我们假设每个单词都用一个300维的向量来表示)
公式化的表示就是:
$$e_j = E \cdot o_j$$
之后,我们把这六个单词进行拼接得到输入模型之中的 $x = [e_4343, e_9665, e_1, e_3852, e_6163, e_6257]$ ,所以 $x \in \mathbb{R}^{1800}$
公式化的表示就是:
$$x_k = [e_{k-6}, e_{k-5}, e_{k-4}, e_{k-3}, e_{k-2}, e_{k-1}]$$
然后,这个 $x$ 被扔进一个多层感知机中,最后一层是 softmax 层,输出的是语料库中每个单词的概率。
$$\hat{y} = P(next|e_{4343}, e_{9665}, e_{1}, e_{3852}, e_{6163}, e_{6257}) = softmax(h W_2 + b_2) \ h = tanh(x W_1 + b_1)$$
那么,想在模型有了,剩下的就是用反向传播把这个模型优化出来就可以了。
经过优化之后,我们可以得到 $W_1$ 、 $b_1$ 、 $W_2$ 、 $b_2$ 、 $E$ 其中 $E$ 就是我们需要的 Embedding Matrix
2.2.1 Word2vec
(1) Skip-gram
该模型的核心思想是:给定中心词预测上下文。

取一个窗口,大小为 $m$, 并且选定一个位置 $t$ 那么我们需要求的是 $p(w_{t-1}|w_t)$、$p(w_{t-2}|w_t)$、… 、$p(w_{t-m}|w_t)$ 和 $p(w_{t+1}|w_t)$、$p(w_{t+2}|w_t)$、… 、$p(w_{t+m}|w_t)$
所以,目标函数是 Negtive log likelihood
模型的训练流程图如下所示:

我们输入的是 one-hot vector, 经过一个 Embedding Matrix $W$ 得到了 dense vector, 然后再乘以一个 $\grave{W}$ 之后经过softmax 操作,得到了我们预测的概率。我们最终的目标是希望,正确 target 的概率值越大越好。
然后按照上面的模型训练一遍语料库,最后得到的 $W$ 就是我们的 Embedding Matrix.
(2) Negtive Sampling
虽然 skip-gram 模型很不错,但是也有很明显的缺陷,就是:在最后的softmax阶段,我们需要计算整个语料库… 开销太大了。
为了能够更加快速、高效地训练出 Word Vectors 我们会采用一种新的训练方式叫 Negtive Sampling
跟前面一样,我们又如下一句话:
I want a glass of orange juice to go along with my cereal
| context | word | target |
|---|---|---|
| orange | juice | 1 |
| orange | king | 0 |
| orange | book | 0 |
| orange | the | 0 |
| orange | of | 0 |
我们随机的选取一个中心词, 然后再从上下文中选择一个词作为 “正例”, 再随机地从整个词库中选择几个词作为 “负例” 然后正例会被我们贴上 $1$ , 负例会被我们贴上 $0$ .
对于小数据集来说,通常我们选择 $k=[5, 20]$ 个负例; 对于大数据集来说,通常我们选择 $k=[2, 5]$ 个负例
然后,我们使用 logstic regression 去训练模型
$$J_t(\theta) = \log \sigma\left(u_o^Tv_c\right)+\sum_{i=1}^k\mathbb{E}_{j \sim P(w)}\left [\log\sigma \left(-u^T_jv_c\right) \right]$$
那么这个目标函数的作用就是要最大化中央词与上下文的相关概率,最小化与其他词语的概率。
另外文中还有几个 trick, emmm…. 不太想讲… 自己去看把,不过友情提示, trick 对于你的模型 work 不 work 是至关重要的。
三、总结
从 one-hot encoding 到 word2vec 再到之后的 Glove 这些方法的本质都是用向量表示单词,最简单的 one-hot encoding 仅仅是考虑的表示单词,而 word2vec 在此基础上更进步能够表示一些相似的单词,但是 word2vec 这样的模型就没有缺陷了么? 我感觉 word2vec 学习 word 之间相似程度的时候依靠的更多的是上下文环境,这样很容易导致单词应该有的“一词多义” 被忽视掉了。而且在不同的数据集上表现也不尽相同,当然,总体来说是一种利好的方法,看那篇论文的引用率也能看出来。